分类：情感分析

本文使用的案例是：分析对餐厅的评价，判断是正面评价还是负面评价

1 分类器（Classifiers）

一个最最原始的分类器是：分别计算每条评论中的积极单词（great，awesome，good，···）和消极单词（terrible，bad，awful，···）的数量，如果积极单词比消极单词多，那么为正面评价，反之则为负面评价。

# Simple threshold classifier

Count positive & negative words in sentence

if number of positive words > number of negative words:
    ŷ =
else:
    ŷ = 

但是上述方法有很多问题：

• 怎样列举积极单词和消极单词？
• 每个单词有不同程度的情感（比如：great > good）
• 只分析单一的单词有很多局限（比如：good 是积极的，not good 是消极的）

2 线性分类器（Linear classifiers）

为了解决上述前两个问题，我们利用训练集来学习每个单词的权重。例如：

Word	Weight
good	1.0
great	1.5
awesome	2.7
bad	-1.0
terrible	-2.1
awful	-3.3
restaurant, the, we, where, …	0.0
…	…

input x：
Sushi was great, the food was awesome, but the service was terrible.
Score(x) = 1.5 + 2.7 - 2.1 = 2.1

我们称其为线性分类器，是因为结果是每个单词的权重之和

# Simple linear classifier

Score(x) = weighted count of words in sentence

if Score (x) > 0:
    ŷ =
else:
    ŷ = 

3 决策边界（Decision boundaries）

如果一个线性分类器只支持 2 个单词：

Word	Weight
awesome	1.0
awful	-1.5

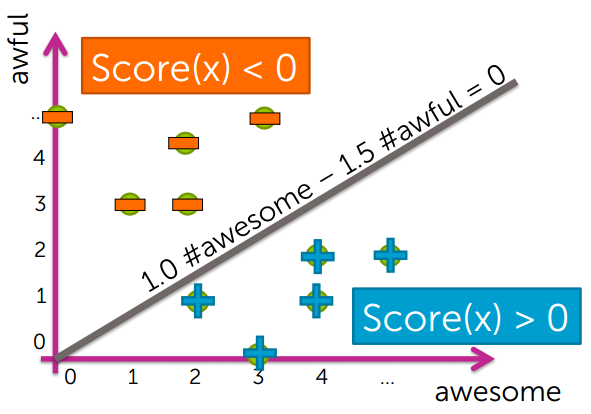
那么 Score(x) = 1.0 #awesome – 1.5 #awful

我们发现它的决策边界是一条直线：

3.1 决策边界的形状

Decision boundary separates positive & negative predictions

• For linear classifiers:
  • When 2 weights are non-zero：line
  • When 3 weights are non-zero：plane
  • When many weights are non-zero：hyperplane
• For more general classifiers
  • more complicated shapes

4 评估分类器（Evaluating classifiers）

4.1 误差率与正确率（error and accuracy）

误差率 error：
$$error = \frac{mistakes}{total}$$
正确率 accuracy：
$$accuracy = \frac{corrects}{total}$$
误差率和正确率的关系：
$$error = 1 - accuracy$$

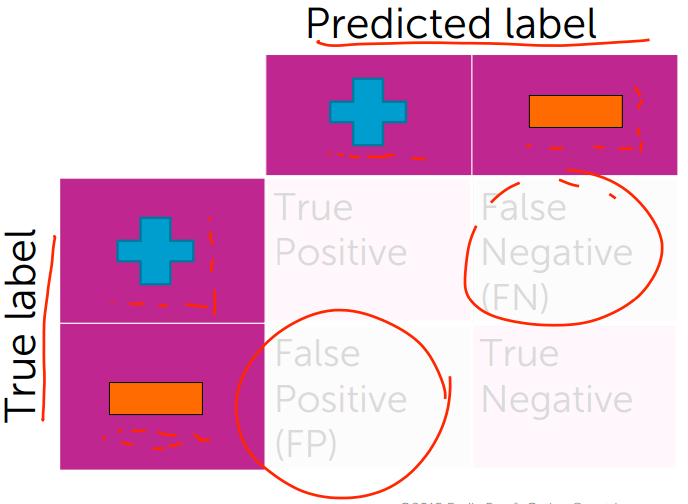
4.2 混淆矩阵（Confusion matrices）

5 学习曲线（Learning curves）

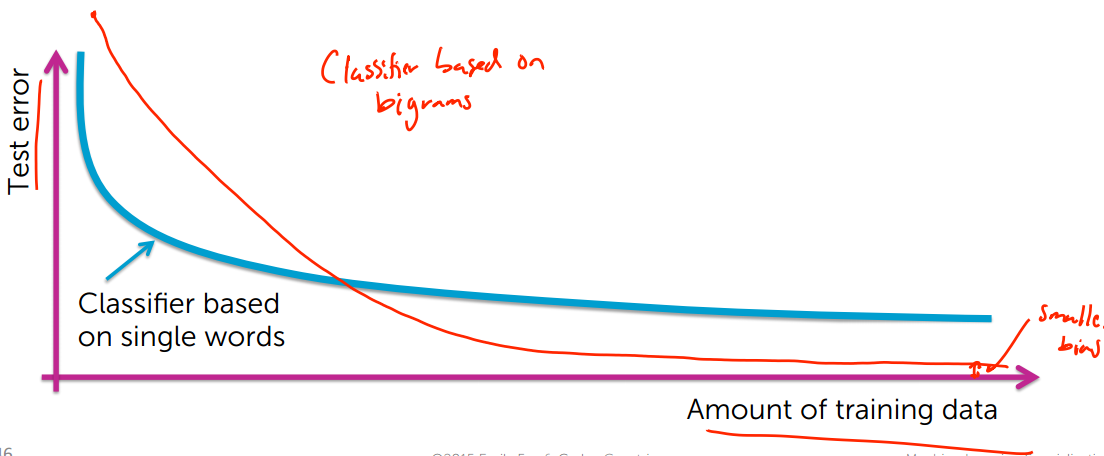
学习曲线把训练数据量和测试误差率联系在一起
随着训练数据增多，测试误差率会越来越低

注：在上图中，蓝色线代表基于单个单词的分类器，红色线代表基于双连词的分类器（就是两个单词连在一起）

一个模型需要学习多少数据和模型复杂度之间的关系：
一般来说，一个模型的参数越多，学习这个模型需要的数据越多

我们从上图也可以分析出，当参数增加（基于双连词的分类器）时，如果数据量不够，那么效果不如参数少的分类器（基于单个单词的分类器），偏差较大；当数据量足够多时，效果好于参数少的分类器，偏差较小，但是也不会为 0。

6 分类概率（Class probabilities）

比如：输入一条评论，输出这条评论的情绪为正或负的概率

7 案例分析：分析 Amazon 婴幼儿产品的评价

代码在这里