二叉搜索树的几何应用

发表于 | 分类于

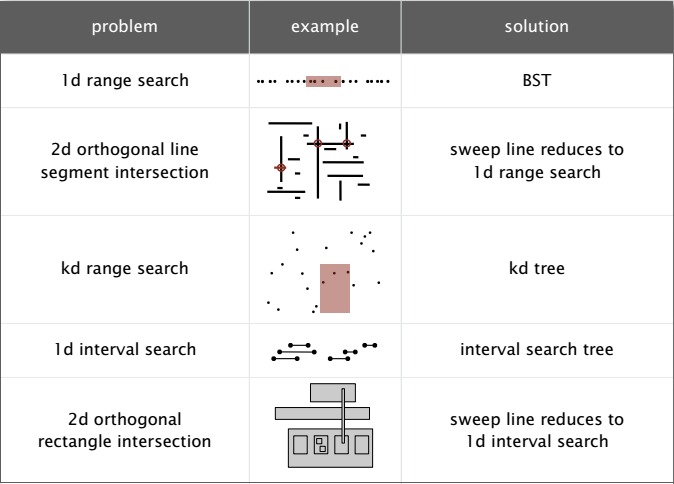
1 概述（Overview）

本文主要讲述几何对象的交点。
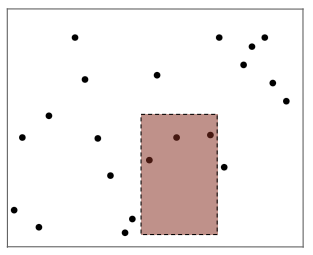
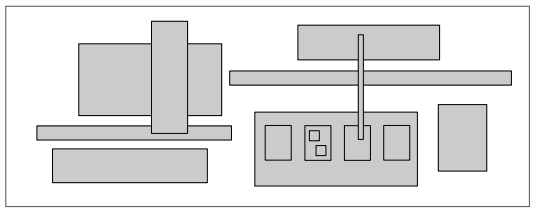
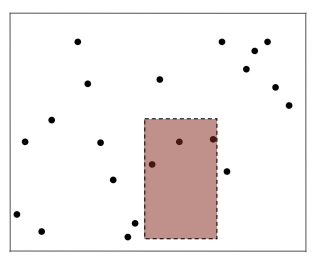
比如，怎样判断一些点是否在指定的边平行于坐标轴的矩形内（如图 1），或者判断一些列矩形是否相交、有多少个交点（如图 2）

GeometricApplicationsOfBSTs_1
GeometricApplicationsOfBSTs_2
应用：CAD、游戏、电影、虚拟现实、数据库、……
高效的解决方案：二叉搜索树（BST）（以及其扩展）

2 一维区间搜索（1d range search）

它是有序符号表（ordered symbol table）的一个小扩展

  • 插入键值对
  • 查找键 k
  • 删除键 k
  • 区间搜索：找出 k1 与 k2 之间的所有键
  • 区间计数：k1 与 k2 之间的所有键的数目

例：

1
2
3
4
5
6
7
8
9
insert B        B
insert D        B D
insert A        A B D
insert I        A B D I
insert H        A B D H I
insert F        A B D F H I
insert P        A B D F H I P
count G to K    2
search G to K   H I

应用：数据库查询

几何解释：

  • 把键看做一条线上的点
  • 在给定的一维区间上找到这些点或给这些点计数

GeometricApplicationsOfBSTs_3

2.1 基本实现

无序列表：插入快，区间搜索慢
有序数组：插入慢，区间搜索用二叉搜索

一位区间搜索运行时间增长：

数据结构 插入 区间计数 区间搜索
无序列表 1 N N
有序数组 N log N R + log N
目标 log N log N R + log N

其中，N = number of keys，R = number of keys that match

2.2 二叉搜索树实现

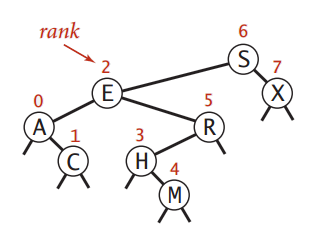
一维区间计数：lo 与 hi 之间有多少个键？（见图 4）
GeometricApplicationsOfBSTs_4

1
2
3
4
5
public int size(Key lo, Key hi)
{
    if (contains(hi)) return rank(hi) - rank(lo) + 1;
    else return rank(hi) - rank(lo); // rank(hi): number of keys < hi
}

命题：运行时间与 log N 成正比
证明：检查的结点数目 = 查找路径到 lo + 查找路径到 hi

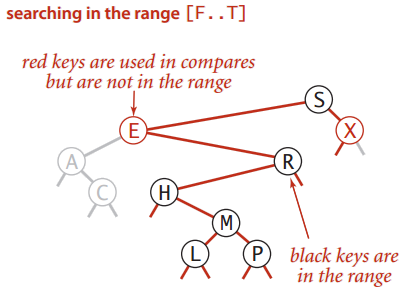
一维区间搜索：找出 lo 与 hi 之间所有键（见图 5）

  • 在左子树递归查找是否有在范围内的键
  • 检查当前结点的键
  • 在右子树递归查找是否有在范围内的键

GeometricApplicationsOfBSTs_5
命题：运行时间与 R + log N 成正比
证明：检查的结点数目 = 查找路径到 lo + 查找路径到 hi + 匹配的数目

3 线段交点（line segment intersection）

3.1 正交线段交点（Orthogonal line segment intersection）

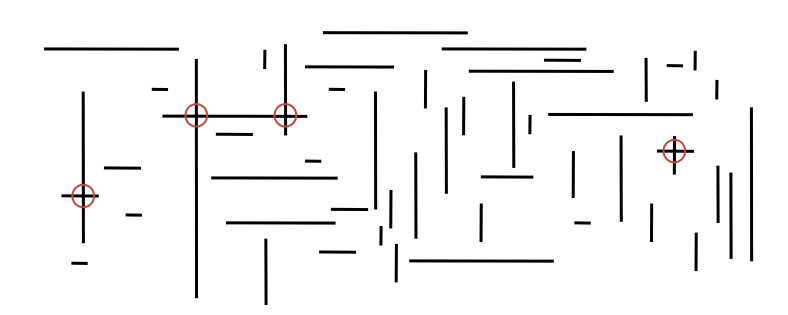
给出 N 条水平或竖直的线段，找出所有交点（如图 6）
GeometricApplicationsOfBSTs_6
二次算法：检查每对线段的交点
非退化线段（Nondegeneracy assumption）：所有 x 轴和 y 轴坐标都不同

3.2 扫描线段法（sweep-line algorithm）

从左向右扫描竖直线段

  • x 轴坐标定义事件
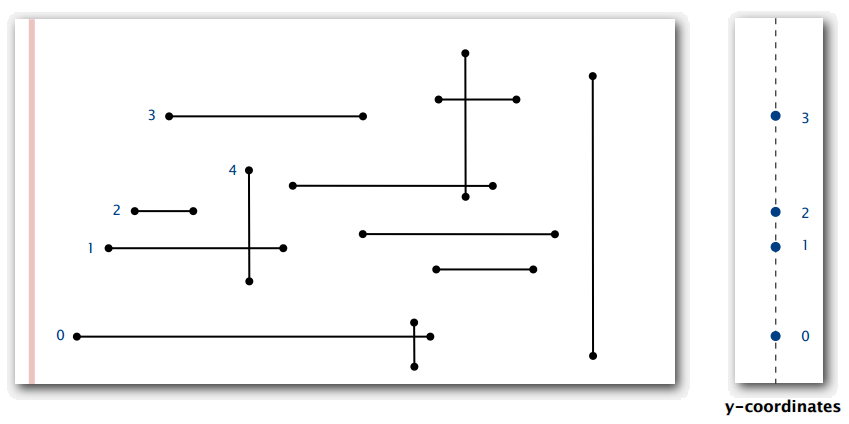
  • 遇到水平线段（左端点）：将其 y 轴坐标插入二叉搜索树（如图 7）
    GeometricApplicationsOfBSTs_7
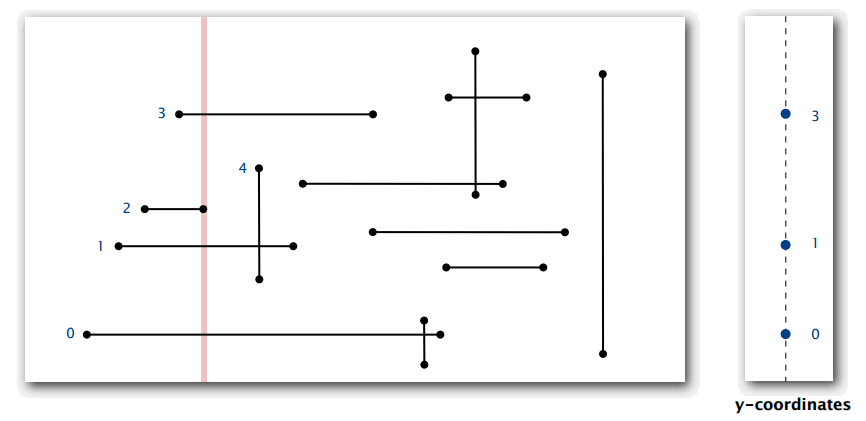
  • 遇到水平线段（右端点）：将其 y 轴坐标从二叉搜索树删除（如图 8）
    GeometricApplicationsOfBSTs_8
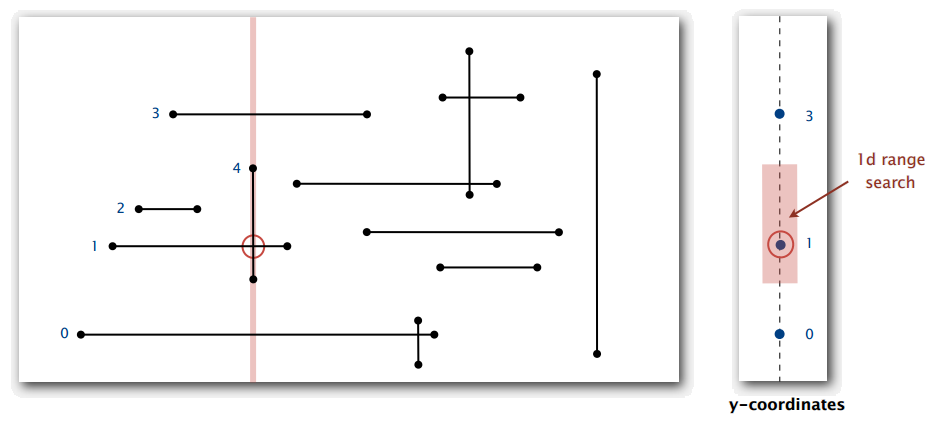
  • 遇到竖直线段：在两个端点的 y 轴坐标之间做区间搜索（如图 9）
    GeometricApplicationsOfBSTs_9

命题：用扫描线段法在 N 条正交线段中找出所有 R 个交点的运行时间与 N log N + R 成正比
证明：

  • 将 x 轴坐标放入一个优先队列（或者排序） <—- N log N
  • 将 y 轴坐标插入二叉搜索树 <—- N log N
  • 将 y 轴坐标从二叉搜索树删除 <—- N log N
  • 在二叉搜索树进行区间搜索 <—- N log N + R

下界：扫描线段法将二维正交线段交点查找降到了一位区间查找

4 kd 树（kd trees）

4.1 二维正交区间搜索（2-d orthogonal range search）

将有序符号表扩展为二维键（可以将二维键想象为二维几何空间中的点）：

  • 插入二维键
  • 删除二维键
  • 查找二维键
  • 区间搜索：找出所有在二维区间中的键
  • 区间计数：所有在二维区间中的键的数目

几何交点（见图 10）：

  • 把键看做平面上的点
  • 在给定的边与坐标轴平行的长方形上找到这些点或给这些点计数

GeometricApplicationsOfBSTs_10
应用：网络、电路设计、数据库、……

4.2 网格实现（grid implementation）

  • 将空间分成 M*M 的方格
  • 创建列表，将每个方格中的点放进去
  • 用二维数组对方格直接编号
  • 插入：将 (x,y) 插入到列表中对应的方格中
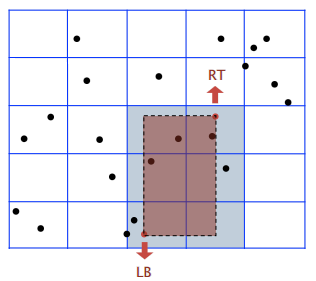
  • 区间搜索：只需要检查与查询的二维区间相交的方格

GeometricApplicationsOfBSTs_11

4.3 网格实现分析（grid implementation analysis）

时间-空间 权衡：

  • 空间：M^2+N
  • 时间：检查每个方格平均需要 1+N/(M^2)

通过选择方格大小来调整性能

  • 太小（M 太大）：浪费空间
  • 太大（M 太小）：每个方格中有太多点
  • 法则：M 大约是 n 的开方

运行时间（如果点是均匀分布的）（当 M~√N）

  • 初始化数据结构：N
  • 插入点：1
  • 区间搜索：范围中的每个点：1

4.4 集群（Clustering）

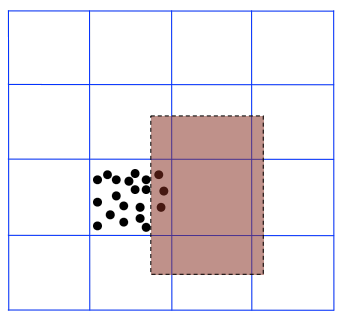
方格实现在平均分布的情况下简洁快速，但是在大多数情况下，这些点并不是均匀分布的，它们会形成集群

集群是一种在几何数据中非常著名的现象，它会使一个列表非常长，虽然平均长度非常短，所以我们需要一个可以适应各种不同数据分布的数据结构

GeometricApplicationsOfBSTs_12

4.5 空间分割树（Space-partitioning trees）

用树来表示递归细分的平面
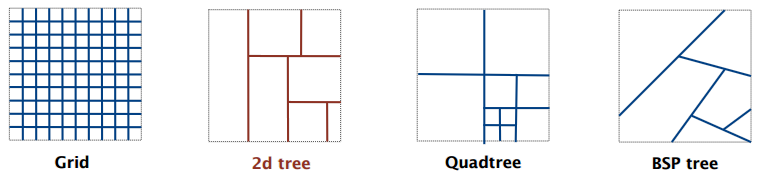
网格（Grid）：将空间均匀地划分为正方形
二维树（2d tree）：递归地将空间分成两个半平面
四维树（Quadtree）：递归地将空间分成四个象限
BSP 树（BSP tree）：递归地将空间划分为两个区域
GeometricApplicationsOfBSTs_13
应用：二维区间搜索，最近邻搜索

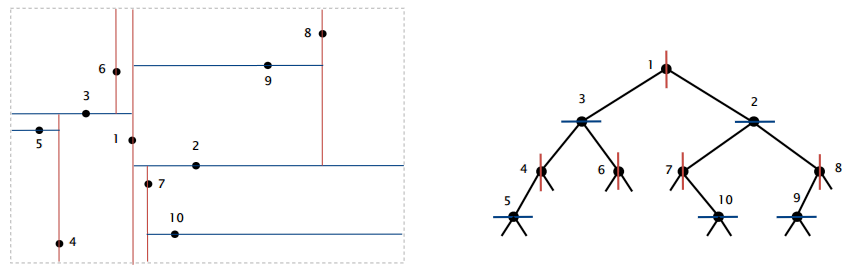
4.6 二维树（2d tree）

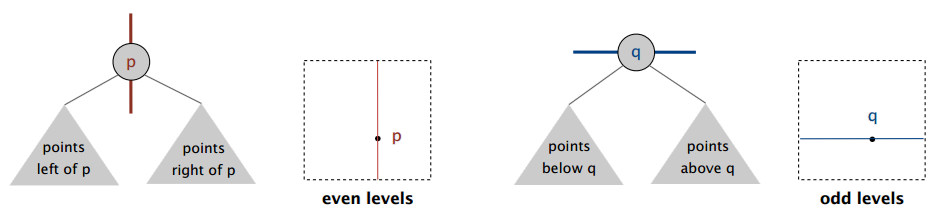
构建：递归地将空间分成两个半平面
GeometricApplicationsOfBSTs_15

数据结构：二叉搜索树，但是交替使用 x 轴坐标和 y 轴坐标作为键

  • 在给定的长方形内搜索点
  • 插入点，进一步细分平面

GeometricApplicationsOfBSTs_14

例 1：二维树的区间搜索
找出所有在边与坐标轴平行的长方形中的点

  • 检查当前结点中的点是否在给定的长方形内
  • 递归检查左/上边（如果它落在了长方形内）
  • 递归检查右/下边（如果它落在了长方形内）

时间复杂度：

  • 典型情况：R+logN
  • 最坏情况（假设树是平衡的）：R + √N

例 2：二维树的最近邻搜索
找出距查询点最近的点

  • 计算当前结点到查询点的距离，如果它是最近的则保存它
  • 递归检查左/上边（如果它包含最近的点）
  • 递归检查右/下边（如果它包含最近的点）

时间复杂度：

  • 典型情况：logN
  • 最坏情况（假设树是平衡的）：N

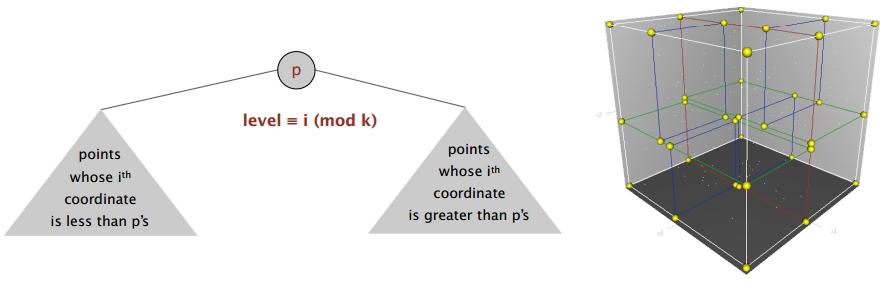
4.7 k 维树（kd tree）

递归地将 k 维空间分成两个半空间
GeometricApplicationsOfBSTs_16
实现：二叉搜索树，用每一维循环分割代替二叉树的水平和竖直交替分割。比如在上图的右图中，用一个平面将一个三维空间分为上和下

这是一个简洁高效的，针对 k 维数据处理的应用广泛的方法：

  • 应用广泛
  • 对高维数据和集群数据适应良好

例 3：N 体模拟（N-body simulation）
目标：模拟 N 个粒子受到相互引力的运动
暴力算法：对于每个粒子，计算力 $F=\frac{Gm_1m_2}{r^2}$
运行时间：每一步的时间为 N^2
关键 idea：如果某些粒子距离某个集群很远，我们可以将那个集群当做一个聚合的粒子，从而不需要计算该群中的每一个粒子与我们的粒子的相互作用力，而是用中心质量计算，可以得到一个对 N 体问题的非常精确的近似

  • 构建一个三维树，将 N 个粒子作为结点
  • 每个结点存放子树的中心质量
  • 要得到总的力，遍历树得到所有信息，完成 N 体计算。时间复杂度更接近 NlgN，而不是 N^2

5 区间搜索树（interval search trees）

5.1 一维区间搜索（1d interval search）

数据结构保存一组区间（可以重合）

  • 插入区间 (lo,hi)
  • 搜索一个区间 (lo,hi)
  • 删除一个区间 (lo,hi)
  • 区间交点查询：给定一个区间 (lo,hi)，找出所有（或一个）与区间 (lo,hi) 相交的区间

API：

1
2
3
4
5
6
   public class IntervalST<Key extends Comparable<Key>, Value>
                IntervalST()                    // create interval search tree
           void put(Key lo, Key hi, Value val)  // put interval-value pair into ST
          Value get(Key lo, Key hi)             // value paired with given interval
           void delete(Key lo, Key hi)          // delete the given interval
Iterable<Value> intersects(Key lo, Key hi)      // all intervals that intersect the given interval

假设：没有两个区间有相同的左端点

5.2 区间搜索树（Interval search trees）

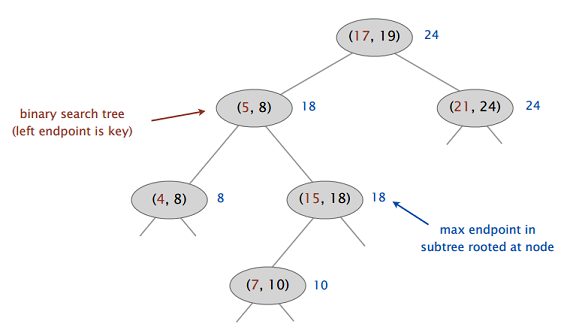
创建一棵二叉搜索树，每个结点存储区间 (lo,hi)（见图 16）

  • 用左端点作为二叉搜索树的键
  • 结点内存放子树根结点中最大的端点

GeometricApplicationsOfBSTs_17

插入区间 (lo,hi)：

  • 在二叉搜索树中插入，将 lo 作为键
  • 更新搜索路径上每个结点的最大端点

搜索任意一个与区间 (lo,hi) 相交的区间：

  • if 当前结点中的区间与查询区间相交，返回它
  • else if 左子树为 null，去右子树
  • else if 左子树的最大端点小于 lo，去右子树
  • else 去左子树
1
2
3
4
5
6
7
8
9
Node x = root;
while (x != null)
{
    if      (x.interval.intersects(lo, hi)) return x.interval;
    else if (x.left == null)                x = x.right;
    else if (x.left.max < lo)               x = x.right;
    else                                    x = x.left;
}
return null;

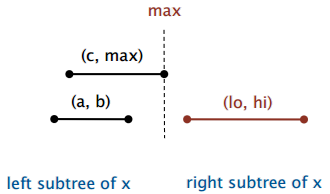
案例 1：如果搜索去了右子树，那么左子树中没有与查询区间相交的区间（见图 18）
证明：如果搜索去了右子树并且左子树不为空

  • 左子树的最大端点 max 比 lo 小
  • 对于 x 的左子树中的任一区间 (a,b)，有 b ≤ max ≤ lo

GeometricApplicationsOfBSTs_18

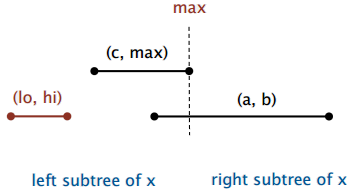
案例 2：如果搜索去了左子树，那么存在一个与查询区间相交的区间在左子树或不存在与查询区间相交的区间（见图 19）
证明：如果左子树中没有与查询区间相交的区间

  • 因为我们去了左子树，所以有 lo≤max
  • 对于 x 的左子树中的任一区间 (a,b)，hi < c ≤ a ⇒ 右子树中不存在与查询区间相交的区间

GeometricApplicationsOfBSTs_19

分析性能：
用红黑二叉搜索树证明其性能（每个操作用额外的 log N 来维护其辅助信息）

order of growth of running time for N intervals:

操作 暴力算法 区间搜索树 best in theory
插入区间 1 log N log N
寻找区间 N log N log N
删除区间 N log N log N
寻找任意一个与区间
(lo,hi)相交的区间		 N log N log N
寻找所有与区间
(lo,hi)相交的区间		 N R log N R + log N

6 矩形交点（rectangle intersection）

6.1 正交矩形交点

目标：从 N 个正交矩形中找出所有交点
二次算法：检查每对矩形的交点
假设：所有矩形的 x 轴坐标和 y 轴坐标都不同

6.2 扫描线算法（sweep-line algorithm）

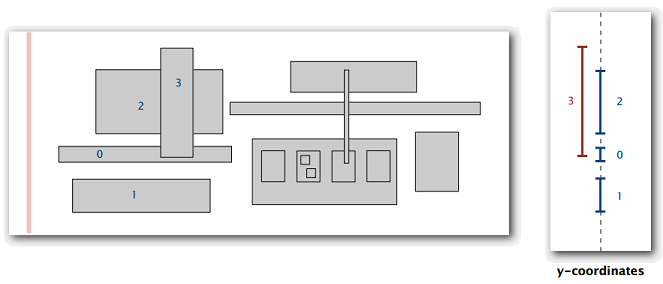
从左向右扫描竖直的线（见图 20）

  • 左右端点的 x 轴坐标定义事件
  • 在一棵区间搜索树中维护与扫描线相交的一组矩形（用矩形的 y 轴区间）
  • 左端点：对矩形的 y 轴区间做区间搜索，插入 y 轴区间
  • 右端点：删除 y 轴区间

GeometricApplicationsOfBSTs_20

命题：用扫描线算法在 N 个矩形中找出 R 个交点的时间与 N log N + R log N 成正比
证明：

  • 将 x 轴坐标放入一个优先队列（或者排序） <—- N log N
  • 将 y 轴坐标插入二叉搜索树 <—- N log N
  • 将 y 轴坐标从二叉搜索树删除 <—- N log N
  • 在二叉搜索树进行区间搜索 <—- N log N + R log N

下界：扫描线段法将二维正交线段交点查找降到了一位区间查找

7 二叉搜索树的几何应用（Geometric applications of BSTs）

GeometricApplicationsOfBSTs_21