优先队列：事件驱动模拟

发表于 | 分类于

1 分子动力学模拟：hard discs 模型（Molecular dynamics simulation of hard discs）

目标：根据弹性碰撞定律（the laws of elastic collision）模拟 n 个运动粒子的运动^1

hard discs 模型：

  • 移动粒子通过相互弹性碰撞以及与墙壁弹性碰撞相互作用
  • 每个粒子都是一个已知位置、速度、质量和半径的圆盘
  • 没有其他力量

意义：涉及到通过宏观（温度，压力，扩散常数）观测微观动力学（单个原子和分子的运动）

  • 麦斯威尔-玻尔兹曼（Maxwell-Boltzmann）：速率分布是温度的函数
  • 爱因斯坦（Einstein）：解释花粉颗粒的布朗运动

2 无碰撞弹球（bouncing balls without the collisions）

事件驱动模拟（Time-driven simulation）：一个独立方格里有 N 个弹球
只根据球的速度和与墙壁的碰撞计算球的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class BouncingBalls
{
    public static void main(String[] args)
    {
        int N = Integer.parseInt(args[0]);
        Ball[] balls = new Ball[N];
        for (int i = 0; i < N; i++)
            balls[i] = new Ball();
        while(true) // main simulation loop
        {
            StdDraw.clear();
            for (int i = 0; i < N; i++)
            {
                balls[i].move(0.5);
                balls[i].draw();
            }
            StdDraw.show(50);   // 每 50 毫秒更新一次
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Ball
{
    private double rx, ry;          // position
    private double vx, vy;          // velocity
    private final double radius;    // radius
    public Ball(...)
    { /* initialize position and velocity */ }
    
    public void move(double dt)
    {
        // check for collision with walls
        if ((rx + vx*dt < radius) || (rx + vx*dt > 1.0 - radius)) { vx = -vx; }
        if ((ry + vy*dt < radius) || (ry + vy*dt > 1.0 - radius)) { vy = -vy; }
        
        rx = rx + vx*dt;
        ry = ry + vy*dt;
    }
    public void draw()
    { StdDraw.filledCircle(rx, ry, radius); }
}

缺点：没有检测球之间的相互碰撞

  • 物理问题：什么时候发生碰撞？碰撞产生的影响？
  • CS 问题：由哪个 object 来检测碰撞？当检测很多时能否将时间复杂度控制在 O(logn)？

3 时间驱动模拟（Time-driven simulation）

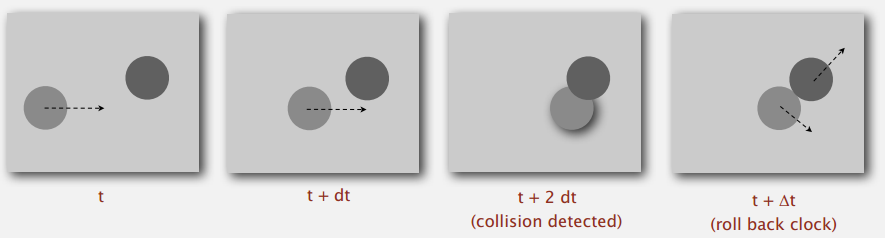
对于 dt 个单位时间，如图 1：

  • 在 dt 个单位时间后，更新每个粒子的位置，并检测是否重叠
  • 如果重叠，回滚到碰撞发生的时刻，更新碰撞粒子的速度，并继续模拟

PriorityQueuesEventDrivenSimulation_1
主要的缺点：

  • 每个时间段需要执行 ~ $\frac{N^2}{2}$ 次重叠检查
  • 如果 dt 太小，模拟会非常慢
  • 如果 dt 太大，可能会错过碰撞

4 事件驱动模拟（Event-driven simulation）

只有当某事发生时才改变状态

  • 在碰撞之间，粒子按轨迹直线运动
  • 只关注碰撞发生的时间
  • 维护一个碰撞事件的优先队列（PQ），按时间排列
  • 删除 min = 得到下一次碰撞（我们从 PQ 中删除的最小元素就是我们下次要处理的碰撞）

碰撞预测（Collision prediction）：给定一个粒子的位置，速度和半径，它下一次和墙壁或另外一个球碰撞发生的时间？
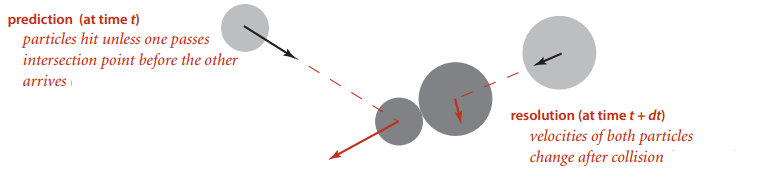
当一个粒子在其它粒子之前通过交叉点，发生碰撞（见图 2）

碰撞处理（Collision resolution）：如果发生碰撞，根据弹性碰撞定律更新碰撞粒子
碰撞后两个粒子的速度均发生变化（见图 2）

PriorityQueuesEventDrivenSimulation_2

4.1 粒子-墙壁 碰撞（Particle-wall collision）

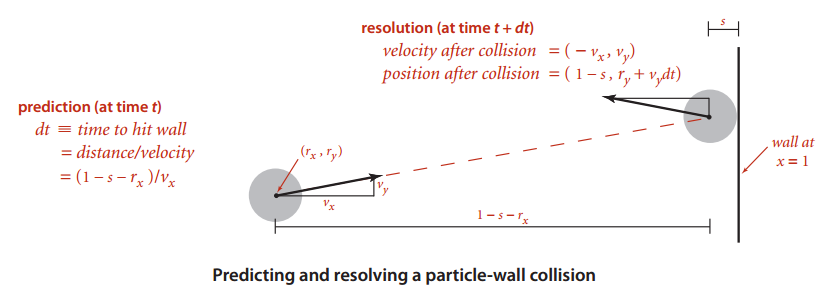
碰撞预测与处理：

  • 粒子半径（radius）为 s，位置为 (rx, ry)
  • 粒子运动速度为 (vx, vy)
  • 它会与垂直的墙壁碰撞吗？如果会，发生在什么时候？

PriorityQueuesEventDrivenSimulation_3

4.2 粒子-粒子 碰撞（Particle-particle collision）

4.2.1 粒子-粒子 碰撞预测（Particle-particle collision prediction）

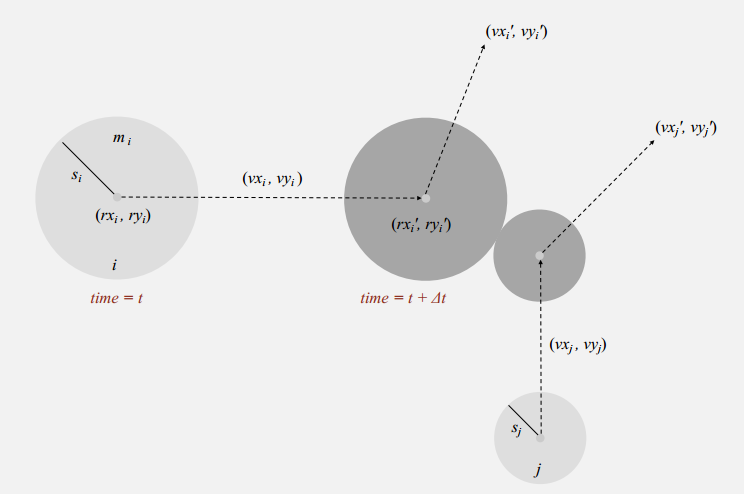
  • 粒子 i：半径 Si，位置 (rxi, ryi)，速度 (vxi, vyi)
  • 粒子 j：半径 Sj，位置 (rxj, ryj)，速度 (vxj, vyj)
  • 粒子 i 与 粒子 j 会发生碰撞吗？如果会，发生在什么时候？

PriorityQueuesEventDrivenSimulation_4

根据牛顿第二定律，可得以下公式：

PriorityQueuesEventDrivenSimulation_5

4.2.2 粒子-粒子 碰撞处理（Particle-particle collision resolution）

当两个粒子发生碰撞，它们的速度怎么变化？

PriorityQueuesEventDrivenSimulation_6

4.3 代码

4.3.1 粒子数据结构框架（Particle data type skeleton）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Particle
{
    private double rx, ry;          // position
    private double vx, vy;          // velocity
    private final double radius;    // radius
    private final double mass;      // mass
    private int count;              // number of collisions
    
    public Particle(...) { }
    
    public void move(double dt) { }
    public void draw()          { }
    
    // predict collision with particle or wall
    public double timeToHit(Particle that)  { }
    public double timeToHitVerticalWall()   { }
    public double timeToHitHorizontalWall() { }
    
    // resolve collision with particle or wall
    public void bounceOff(Particle that)    { }
    public void bounceOffVerticalWall()     { }
    public void bounceOffHorizontalWall()   { }
}

4.3.2 粒子-粒子 碰撞预测与处理（Particle-particle collision and resolution implementation）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public double timeToHit(Particle that)
{
    if (this == that) return INFINITY;
    double dx = that.rx - this.rx, dy = that.ry - this.ry;
    double dvx = that.vx - this.vx; dvy = that.vy - this.vy;
    double dvdr = dx*dvx + dy*dvy;
    if( dvdr > 0) return INFINITY;  // no collision
    double dvdv = dvx*dvx + dvy*dvy;
    double drdr = dx*dx + dy*dy;
    double sigma = this.radius + that.radius;
    double d = (dvdr*dvdr) - dvdv * (drdr - sigma*sigma);
    if (d < 0) return INFINITY; //no collision
    return -(dvdr + Math.sqrt(d)) / dvdv;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void bounceOff(Particle that)
{
    double dx = that.rx - this.rx, dy = that.ry - this.ry;
    double dvx = that.vx - this.vx, dvy = that.vy - this.vy;
    double dvdr = dx*dvx + dy*dvy;
    double dist = this.radius + that.radius;
    double J = 2 * this.mass * that.mass * dvdr / ((this.mass + that.mass) * dist);
    double Jx = J * dx / dist;
    double Jy = J * dy / dist;
    this.vx += Jx / this.mass;
    this.vy += Jy / this.mass;
    that.vx -= Jx / that.mass;
    that.vy -= Jy / that.mass;
    this.count++;
    that.count++;
}

4.3.3 碰撞系统（Collision system）

初始化（Initialization）（时间复杂度 O(N^2)，只用执行一次）：

  • 用所有潜在的粒子-墙壁碰撞填充 PQ
  • 用所有潜在的粒子-粒子碰撞填充 PQ
    （潜在的：由于其它粒子碰撞干涉，碰撞可能不会发生）
    PriorityQueuesEventDrivenSimulation_7

主循环（Main loop）：

  • 从 PQ 中删除即将发生的事件（min 的优先级为 t）
  • 如果事件已经失效，忽略它
  • 推进所有的粒子的直线轨迹到时刻 t
  • 更新碰撞粒子的速度（s）
  • 预测发生碰撞的粒子的未来的粒子-墙壁、粒子-粒子碰撞，并将事件插入 PQ

Event 数据结构（Event data type）：
约定：

  • 两个粒子都不是 null ⇒ 粒子-粒子碰撞
  • 一个粒子是 null ⇒ 粒子-墙壁碰撞
  • 两个粒子都是 null ⇒ 重新绘制 event
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private class Event implements Comparable<Event>
{
    private double time;        // time of event
    private Particle a, b;      // particles involved in event
    private int countA, countB; // collision counts for a and b
    
    // create event
    public Event(double t, Particle a, Particle b) { }
    
    // ordered by time
    public int compareTo(Event that)
    { return this.time - that.time; }
    
    // invalid if intervening collision
    public boolean isValid()
    { }
}

碰撞系统实现：框架（Collision system implementation: skeleton）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class CollisionSystem
{
    private MinPQ<Event> pq;        // the priority queue
    private double t = 0.0;         // simulation clock time
    private Particle[] particles;   // the array of particles
    
    public CollisionSystem(Particle[] particles) { }
    
    // add to PQ all particle-wall and particleparticle collisions involving this particle
    private void predict(Particle a)
    {
        if (a == null) return;
        for (int i = 0; i < N; i++)
        {
            double dt = a.timeToHit(particles[i]);
            pq.insert(new Event(t + dt, a, particles[i]));
        }
        pq.insert(new Event(t + a.timeToHitVerticalWall() , a, null));
        pq.insert(new Event(t + a.timeToHitHorizontalWall(), null, a));
    }
    
    private void redraw() { }
    
    public void simulate() { /* see next slide */ }
}

碰撞系统实现：事件驱动模拟主循环（Collision system implementation: main event-driven simulation loop）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public void simulate()
{
    // initialize PQ with collision events and redraw event
    pq = new MinPQ<Event>();
    for(int i = 0; i < N; i++) predict(particles[i]);
    pq.insert(new Event(0, null, null));
    
    while(!pq.isEmpty())
    {
        // get next event
        Event event = pq.delMin();
        if(!event.isValid()) continue;
        Particle a = event.a;
        Particle b = event.b;
        
        // update positions and time
        for(int i = 0; i < N; i++)
            particles[i].move(event.time - t);
        t = event.time;
        
        // process event
        if      (a != null && b != null) a.bounceOff(b);
        else if (a != null && b == null) a.bounceOffVerticalWall()
        else if (a == null && b != null) b.bounceOffHorizontalWall();
        else if (a == null && b == null) redraw();
        
        // predict new events based on changes
        predict(a);
        predict(b);
    }
}