8 数码问题

发表于 | 分类于

本次作业为写一个程序使用 A* 搜索算法解决 8 数码问题（8-puzzle problem）

1 问题（The problem）

8-puzzle 问题[^1]是 Noyes Palmer Chapman 在 1870s 年发明和推广的一个难题。它由从 1 到 8 的 8 个方块和 1 个空白方格组成 1 个 3*3 的网格。我们的目标是通过尽可能少的移动重新排列方块，使它们顺着数字的次序排列。允许水平或垂直滑动方块进入空白方格。下面展示了从初始情况（左）到最终目标情况（右）的一系列合法移动。

1
2
3
4
   1  3        1     3        1  2  3        1  2  3        1  2  3
4  2  5   =>   4  2  5   =>   4     5   =>   4  5      =>   4  5  6
7  8  6        7  8  6        7  8  6        7  8  6        7  8 
initial        1 left          2 up          5 left          goal

2 最佳优先搜索（Best-first search）

现在，我们描述了一个问题的解决方案，被称为 A* 搜索算法^2的一个人工智能常用方法。
我们定义游戏的一个搜索节点为一个 board、达到这个节点时移动的次数、前一个搜索节点。首先，我们将初始搜索节点（初始 board、0 次移动、一个为 null 的前搜索节点）插入优先队列。然后，从优先队列中删除优先级最小的搜索节点，并将所有相邻的搜索节点（从出队列的搜索节点移动一次就可以到达的）插入优先队列。重复这个过程直到出队列的搜索节点与目标 board 相对应。这种方法是否可行取决于搜索节点的优先级函数。我们在此考虑两个优先级函数：

  • Hamming 优先级函数
    错误位置方块的数量，加上到达本搜索节点时移动的次数。直观地说，一个有少量错误位置方块的搜索节点更接近于目标，我们更希望使用移动次数较少就可以到达的搜索节点。
  • Manhattan 优先级函数
    方块与它们目标位置的 Manhattan 距离的总和（垂直距离与水平距离的总和），加上到达本搜索节点时移动的次数。
    例如，下面的初始搜索节点的 Hamming 优先级与 Manhattan 优先级分别是 5 和 10
    1
    2
    3
    4
    5
    8  1  3        1  2  3     1  2  3  4  5  6  7  8    1  2  3  4  5  6  7  8
    4     2        4  5  6     ----------------------    ----------------------
    7  6  5        7  8        1  1  0  0  1  1  0  1    1  2  0  0  2  2  0  3

    initial          goal         Hamming = 5 + 0          Manhattan = 10 + 0
    我们可以观察出一个很关键的事情：从优先队列中给定的一个搜索节点解决该问题，需要移动的最少次数（包括已经发生的移动）是它使用 Hamming 或 Manhattan 优先级函数得到的优先级。（对于 Hamming 优先级，每个错误位置的方块必须移动至少一次才能到达它的目标位置。对于 Manhattan 优先级，每个错误位置的方块必须至少移动的次数为到目标位置的 Manhattan 距离。注意，计算 Hamming 或 Manhattan 优先级时不计算空白方格。）因此，当目标 board 出队列，我们不仅可以得到从初始 board 到目标 board 发生的一系列移动，也可以得到移动次数最少的方案。（数学方面的挑战：证明这一事实）

3 一个关键的优化（A critical optimization）

最佳优先搜索有一个令人烦恼的特性：对应相同 board 的搜索节点往往会被插入优先队列很多次。为了减少没用的搜索节点的不必要的搜索，考虑一个搜索节点的相邻节点时，与前搜索节点的 board 相同的相邻节点不要再次入列。

1
2
3
4
5
8  1  3       8  1  3       8  1       8  1  3     8  1  3
4     2       4  2          4  2  3    4     2     4  2  5
7  6  5       7  6  5       7  6  5    7  6  5     7  6

previous    search node    neighbor   neighbor    neighbor

4 游戏树（Game tree）

可视化计算的一种方法是画出树，每个搜索节点都是树的一个节点，一个节点的子节点表示它的相邻搜索节点。树的根节点表示初始搜索节点；内部节点已经处理完毕；叶子结点在优先队列里；在每一步，A* 算法从优先队列中删除优先级最小的节点，并处理它（将它的子节点加在树和优先队列中）。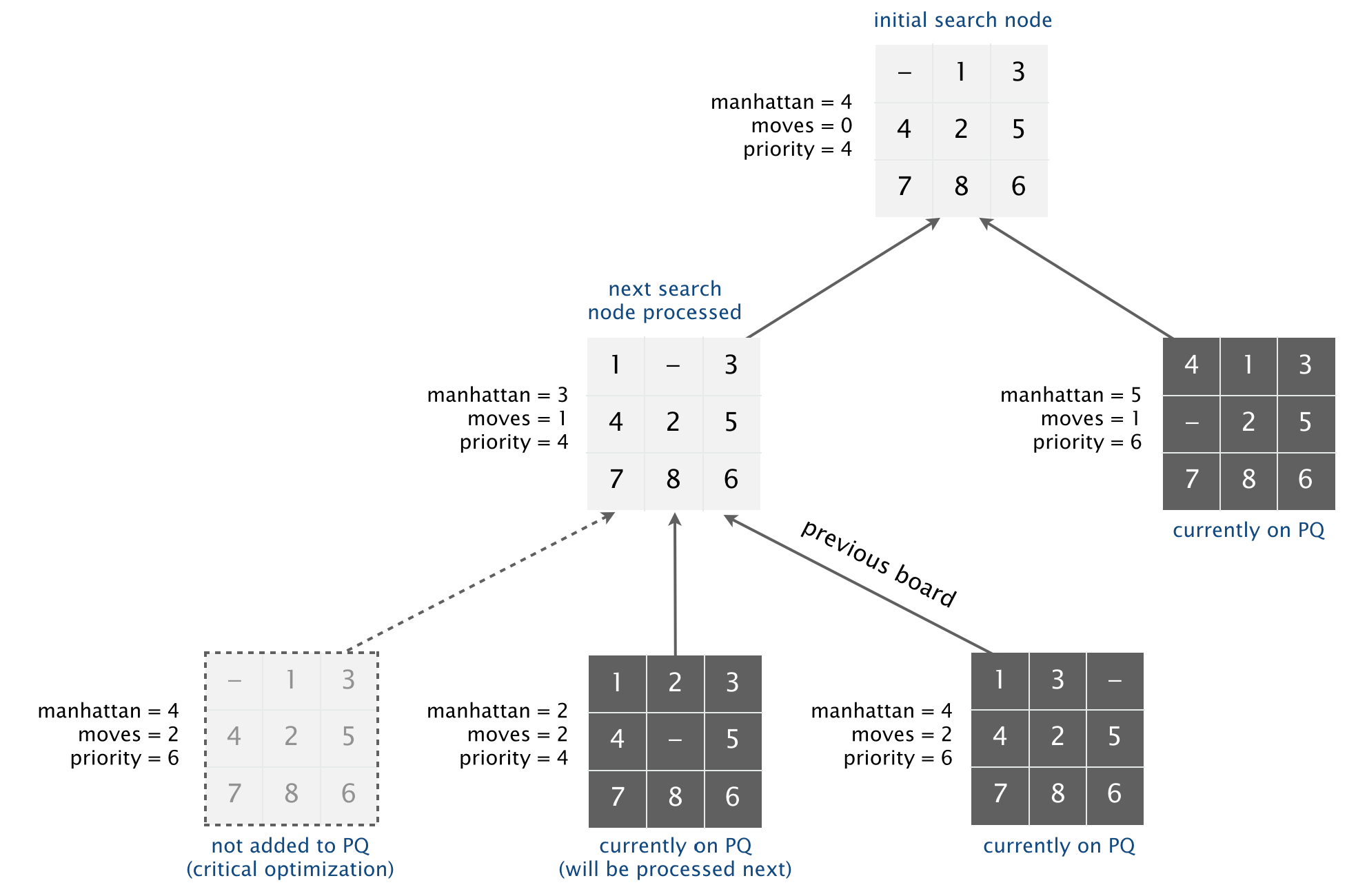
8puzzle-game-tree

5 检测无法解决的问题（Detecting unsolvable puzzles）

并不是所有的初始 board 都可以通过一系列合法移动到达目标 board，比如下面两个：

1
2
3
4
5
6
1  2  3         1  2  3  4
4  5  6         5  6  7  8
8  7            9 10 11 12
               13 15 14 

unsolvable      unsolvable

为了检测这种情况，我们将可达的 board 分为两个等价类：（i）可以到达目标 board 的（ii）如果我们在初始 board 交换任意一对方块（空白方格不算一个方块）可以到达目标 board 的。（数学方面的较难的挑战：证明这个事实。）应用这个事实，在两个实例执行 A* 算法——一个是初始 board，一个是交换一对方块后的初始 board——同步运行。两个中只有一个能够到达目标 board。

6 Board 和 Solver 数据类型

6.1 Board 数据类型

使用下面的 API 创建一个不可变的数据类型 Board：

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Board {
    public Board(int[][] blocks)           // construct a board from an n-by-n array of blocks
                                           // (where blocks[i][j] = block in row i, column j)
    public int dimension()                 // board dimension n
    public int hamming()                   // number of blocks out of place
    public int manhattan()                 // sum of Manhattan distances between blocks and goal
    public boolean isGoal()                // is this board the goal board?
    public Board twin()                    // a board that is obtained by exchanging any pair of blocks
    public boolean equals(Object y)        // does this board equal y?
    public Iterable<Board> neighbors()     // all neighboring boards
    public String toString()               // string representation of this board (in the output format specified below)
    public static void main(String[] args) // unit tests (not graded)
}

6.1.1 极端案例（Corner cases）

你可以假设构造函数接收一个包括从 0 到 n^2-1 的 n^2 个整数的 n*n 数组，0 代表空白方格。

6.1.2 性能要求（Performance requirements）

Board 的所有方法的最坏时间复杂度不超过 n^2

6.2 Solver 数据类型

同样，使用下面的 API 创建一个不可变的数据类型 Board：

1
2
3
4
5
6
7
public class Solver {
    public Solver(Board initial)           // find a solution to the initial board (using the A* algorithm)
    public boolean isSolvable()            // is the initial board solvable?
    public int moves()                     // min number of moves to solve initial board; -1 if unsolvable
    public Iterable<Board> solution()      // sequence of boards in a shortest solution; null if unsolvable
    public static void main(String[] args) // solve a slider puzzle (given below)
}

为了实现 A* 算法，你必须使用 algs4.jar 中的 MinPQ 来实现优先队列

6.2.1 极端案例（Corner cases

如果构造函数的参数为 null，抛出异常 java.lang.NullPointerException

7 Solver test client

使用下面的 test client 从一个文件（用命令行参数指定）中读取 puzzle，并在标准输出打印出解决方案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static void main(String[] args) {
    // create initial board from file
    In in = new In(args[0]);
    int n = in.readInt();
    int[][] blocks = new int[n][n];
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            blocks[i][j] = in.readInt();
    Board initial = new Board(blocks);
    // solve the puzzle
    Solver solver = new Solver(initial);
    // print solution to standard output
    if (!solver.isSolvable())
        StdOut.println("No solution possible");
    else {
        StdOut.println("Minimum number of moves = " + solver.moves());
        for (Board board : solver.solution())
            StdOut.println(board);
    }
}

8 输入输出格式（Input and output formats）

一个 board 的输入输出格式为一个维数 n，后面跟一个 n*n 的初始 board，用 0 表示空白方格。例子如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
% more puzzle04.txt
3
 0  1  3
 4  2  5
 7  8  6
% java Solver puzzle04.txt
Minimum number of moves = 4
3
 0  1  3 
 4  2  5 
 7  8  6 
3
 1  0  3 
 4  2  5 
 7  8  6 
3
 1  2  3 
 4  0  5 
 7  8  6 
3
 1  2  3 
 4  5  0   
 7  8  6 
3
 1  2  3 
 4  5  6 
 7  8  0
% more puzzle3x3-unsolvable.txt
3
 1  2  3
 4  5  6
 8  7  0
% java Solver puzzle3x3-unsolvable.txt
No solution possible

你的程序应该可以解决任意 n*n 的 board（2 ≤ n ＜128），虽然解决它们之中的一些非常慢，需要花费一些合理的时间

9 解决方案（Solutions）

  1. 怎样实现 equals()？
    在 java 中，实现 equals() 需要遵守一些规则。详细的讲解可以参照《算法（第 4 版）》中文翻译版第 65 页、英文原版第 103 页
  2. I run out of memory when running some of the large sample puzzles. What should I do?
    Be sure to ask Java for additional memory, e.g., java -Xmx1600m Solver puzzle36.txt. We recommend running from the command line (and not from the DrJava interaction pane). You should expect to run out of memory when using the Hamming priority function. Be sure not to put the JVM option in the wrong spot or it will be treated as a command-line argument, e.g., java Solver -Xmx1600m puzzle36.txt.
  3. My program can’t solve some of the 4-by-4 puzzles, even if I give it a huge amount of space. What am I doing wrong?
    Probably nothing. The A* algorithm (with the Manhattan priority function) will struggle to solve even some 4-by-4 instances.

优化：

  • Java 中的 char 类型是16字节的，因此 Board 类中的二维数组可以换成 char 类型的。更进一步地，换成大小为 N^2 的一维数组，占用的内存会更少
  • 将 board 的 Manhattan 距离保存下来（或者保存搜索节点的）
  • Exploit the fact that the difference in Manhattan distance between a board and a neighbor is either −1 or +1.（还没看明白=_=）
  • 使用 1 个优先队列
  • 当两个搜索节点的 Manhattan 优先级相同时，你可以随意决定选哪个。比如：比较它们两个对应的 board 的 Manhattan 距离
  • 使用别的方法判断问题是否无解。比如初始 board 的逆序数的奇偶性
  • 使用 IDA* 搜索或双向搜索

10 代码

见 GitHub 的 repo：**PrincetonAlgs4**

  • Board.java
  • Solver.java（使用 Manhattan 优先级）
    本作业不使用除 java.lang，java.util，和 algs4.jar 以外的 library。

11 分析运行时间和占用内存（Analysis of running time and memory usage）

见分析报告

[^1]: 中文维基百科： https://zh.wikipedia.org/wiki/%E6%95%B8%E5%AD%97%E6%8E%A8%E7%9B%A4%E9%81%8A%E6%88%B2
英文维基百科：https://en.wikipedia.org/wiki/15_puzzle

英文维基百科：https://en.wikipedia.org/wiki/A*_search_algorithm