归并排序：共线点

此次作业[^1]需要编写一个程序来识别给定的一组点中的线段
计算机视觉包括分析视觉图像中的模式并重建产生它们的真实物体。该过程通常分为两个阶段：特征检测和模式识别。特征检测包括选择图像的重要特征；模式识别涉及到发现特征的模式。我们将研究一个特别简单的模式识别问题，涉及点和线段。这种模式识别出现在许多其他应用中，如统计数据分析。

1 问题（The problem）

给出平面上不重合的 n 个点，找出每条连接了其中 4 个或更多点的（最长的）线段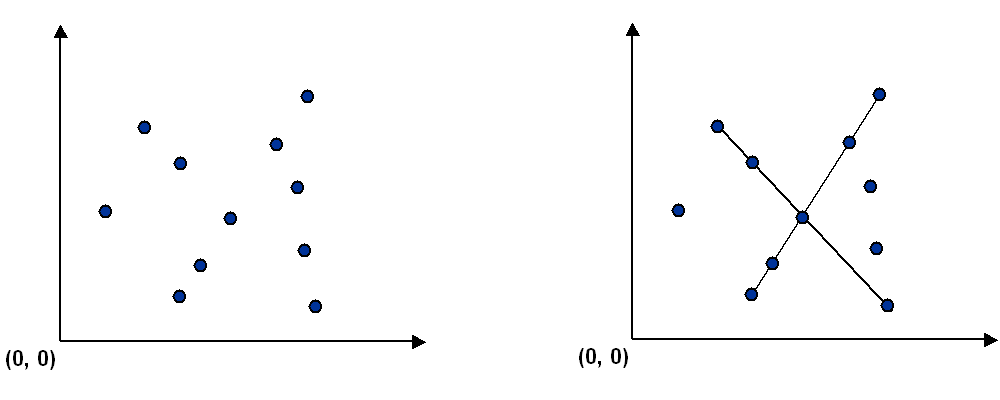
MergesortCollinearPoints_1

2 点的数据结构（Point data type）

2.1 数据结构（Data type）

public class Point implements Comparable<Point> {
   public Point(int x, int y)                         // constructs the point (x, y)

   public   void draw()                               // draws this point
   public   void drawTo(Point that)                   // draws the line segment from this point to that point
   public String toString()                           // string representation

   public               int compareTo(Point that)     // compare two points by y-coordinates, breaking ties by x-coordinates
   public            double slopeTo(Point that)       // the slope between this point and that point
   public Comparator<Point> slopeOrder()              // compare two points by slopes they make with this point
}

其中 constructor、draw()、drawTo()、toString() 的代码都已给出，我们的任务是以下部分：

compareTo() 方法：首先根据 y 轴坐标，其次根据 x 轴坐标比较两个点。正常情况下，当且仅当 y0 < y1，或 y0 = y1 且 x0 < x1，点 (x0,y0) 小于点 (x1,y1)
slopeTo() 方法：返回点 (x0,y0) 和参数点 (x1,y1)之间的斜率，公式为 *(y1 − y0) / (x1 − x0)*。水平线段的斜率为 +0；竖直线段的斜率为正无穷；退化线段（一个点与它本身之间的线段）斜率为负无穷
slopeOrder() 方法：返回两个参数点分别与点 (x0,y0) 之间的斜率的比较。正常情况下，当且仅当斜率 (y1 − y0) / (x1 − x0) 小于斜率 (y2 − y0) / (x2 − x0)，点 (x0,y0) 小于点 (x1,y1)。对待水平线段、竖直线段、退化线段的方法与 slopeTo() 相同
不要复写 equals() 或 hashCode() 方法

2.2 极端案例（Corner cases）

为了避免整数溢出与浮点数精度引发的潜在问题，你可以假设 constructor 的参数 x 和 y 均在 0 到 32,767 之间

3 线段的数据结构（Line segment data type）

public class LineSegment {
   public LineSegment(Point p, Point q)        // constructs the line segment between points p and q
   public   void draw()                        // draws this line segment
   public String toString()                    // string representation
}

所有 API 均已给出

4 暴力算法（Brute force）

4.1 数据结构（Data type）

写一个 BruteCollinearPoints.java，每次检测 4 个点是否共线，返回所有这样的线段。为了检测 4 个点 p、q、r、s 是否共线，检测 3 个斜率：p，q 之间、p，r 之间、p，s 之间是否全部相等

public class BruteCollinearPoints {
   public BruteCollinearPoints(Point[] points)    // finds all line segments containing 4 points
   public           int numberOfSegments()        // the number of line segments
   public LineSegment[] segments()                // the line segments
}

segments() 方法：需要包含每个含有 4 个点的线段。如果一条线段为 p→q→r→s，那么 segments() 方法需要包括线段 p→s 或 s→p（但是不同时包括这两个），而且不包括 p→r 或 q→r 这样的线段。为了简单起见，我们将不为 BruteCollinearPoints 提供任何 5 或更多点共线的输入

4.2 极端案例（Corner cases）

如果 constructor 的参数为 null 或者数组中的任意一点为 null，抛出异常 java.lang.NullPointerException
如果 constructor 的参数包含重复的点，抛出异常 java.lang.IllegalArgumentException

4.3 性能要求（Performance requirement）

最坏时间复杂度为 O(n^4)
使用内存与（n + 返回的线段的数目）成正比

5 一个更快的，基于排序的解决方案（A faster, sorting-based solution）

5.1 算法

很明显，有比以上的暴力算法更快的解决方案。给出点 p，以下方法可以判断 p 是否是 4 点或更多点共线的集合中的点

将 p 当成原点
对于其它的点 q，计算它与点 p 之间的斜率
根据点与点 p 之间的斜率将点排序
检查在序列中是否有相邻的 3 点或更多点与点 p 之间的斜率相同，如果有，这几个点和点 p 是共线的

依次为 n 个点中的每个点执行此方法
这个算法更快是因为排序这一关键操作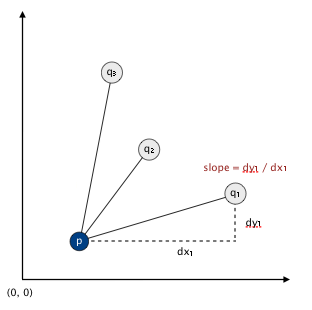
MergesortCollinearPoints_2

写一个 FastCollinearPoints.java 实现此算法

public class FastCollinearPoints {
   public FastCollinearPoints(Point[] points)     // finds all line segments containing 4 or more points
   public           int numberOfSegments()        // the number of line segments
   public LineSegment[] segments()                // the line segments
}

segments() 方法：需要包括每个 4 点或更多点贡献的最长线段。例如，如果如果有 5 点共线的线段 p→q→r→s→t，那么不要包括子线段 p→s 或 q→t

5.2 极端案例（Corner cases）

5.3 性能要求（Performance requirement）

最坏时间复杂度为 O(n^2)
使用内存与（n + 返回的线段的数目）成正比
FastCollinearPoints 需要可以检测出 5 点或更多点共线的输入情况

6 Sample client

client 程序有一个文件名作为命令行参数；读取文件（格式如下所描述）；在标准输出的每一行打印出一条程序发现的线段；在标准绘图画出线段

public static void main(String[] args) {

    // read the n points from a file
    In in = new In(args[0]);
    int n = in.readInt();
    Point[] points = new Point[n];
    for (int i = 0; i < n; i++) {
        int x = in.readInt();
        int y = in.readInt();
        points[i] = new Point(x, y);
    }

    // draw the points
    StdDraw.enableDoubleBuffering();
    StdDraw.setXscale(0, 32768);
    StdDraw.setYscale(0, 32768);
    for (Point p : points) {
        p.draw();
    }
    StdDraw.show();

    // print and draw the line segments
    BruteCollinearPoints collinear = new BruteCollinearPoints(points);
    for (LineSegment segment : collinear.segments()) {
        StdOut.println(segment);
        segment.draw();
    }
    StdDraw.show();
}

7 输入格式（Input format）

题目提供了几个输入样例文件（与上述 client 相配），格式如下：一个整数 n，后面跟 n 对整数 (x, y)，均在 0 到 32,767 之间。以下是两个例子：

% more input6.txt       % more input8.txt
6                       8
19000  10000             10000      0
18000  10000                 0  10000
32000  10000              3000   7000
21000  10000              7000   3000
 1234   5678             20000  21000
14000  10000              3000   4000
                         14000  15000
                          6000   7000
% java BruteCollinearPoints input8.txt
(10000, 0) -> (0, 10000) 
(3000, 4000) -> (20000, 21000) 

% java FastCollinearPoints input8.txt
(3000, 4000) -> (20000, 21000) 
(0, 10000) -> (10000, 0)

% java FastCollinearPoints input6.txt
(14000, 10000) -> (32000, 10000)

8 解决方案（Solutions）

8.1 BruteCollinearPoints.java

只要遍历所有 $C_N^4$ 种可能的组合并判断是否在一条直线上即可。遍历的方法是使用嵌套的for循环（4个套在一起）；因此，有一种简单的降低复杂度的方法，即先判断前三个点是否共线，如果不共线就不再找第四个点了。这样可以使大部分输入数据的时间复杂度降到O(N^3)。

8.2 FastCollinearPoints.java

避免输出子线段和重复线段：
每次得到一条线段上的所有点后，排序，当且仅当排序后第一个点是p时输出

9 代码

见 GitHub 的 repo：PrincetonAlgs4

BruteCollinearPoints.java
FastCollinearPoints.java
Point.java

10 分析运行时间和占用内存（Analysis of running time and memory usage）

见分析报告

[^1]: 原文见 http://coursera.cs.princeton.edu/algs4/assignments/collinear.html
也可以从网站 http://introcs.cs.princeton.edu/java/assignments/ 找到