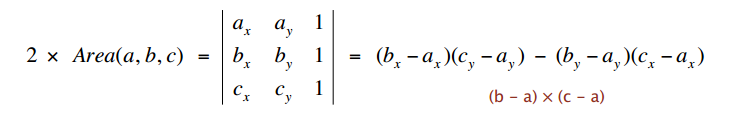凸包问题

发表于 | 分类于

1 凸包（Convex hull）

凸包：假设平面上有 n 个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，我们就叫它“凸包”

ConvexHull_1
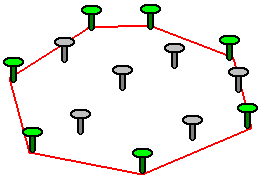
凸包问题：给出点的数目和各个点的坐标，求构成凸包的点

2 凸包应用（Convex hull application）

2.1 应用 1：运动规划（motion planning）

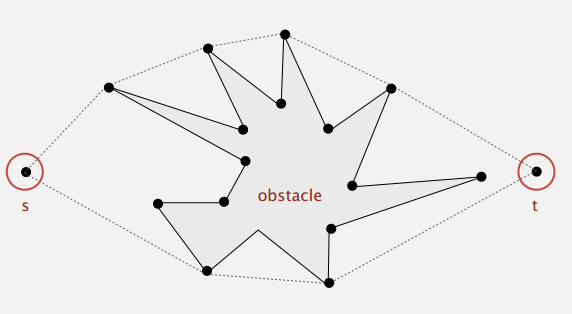
机器人运动规划：寻找可以从点 s 到点 t 的能够避开多边形障碍物的最短路径
ConvexHull_2
最短路径是 s 到 t 的直线或者是凸包的两条路线之一

2.2 应用 2：最远配对（farthest pair）

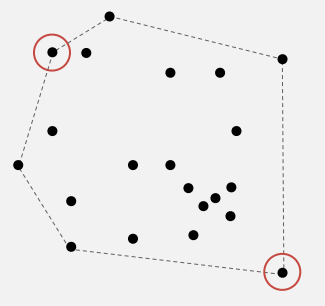
最远配对问题：给出平面上的 N 个点，从中选出欧氏距离最大的一对点
ConvexHull_3
最远的点一定是凸包的顶点

3 Graham 扫描法

选取纵坐标最小的点作为起点，如图 4 中的 P0
按照以 p0 为起点的极角从小到大的顺序，将其它所有的点进行排序
依次考虑每个点：如果可以产生一个逆时针旋转（counterclockwise turn），就留下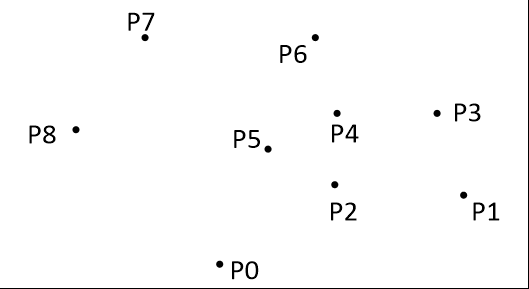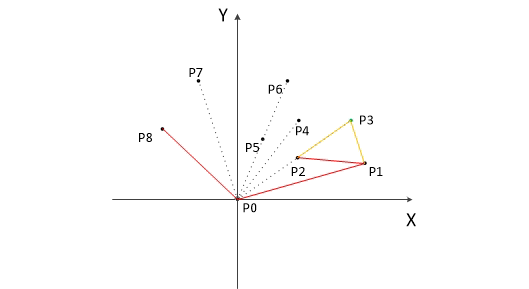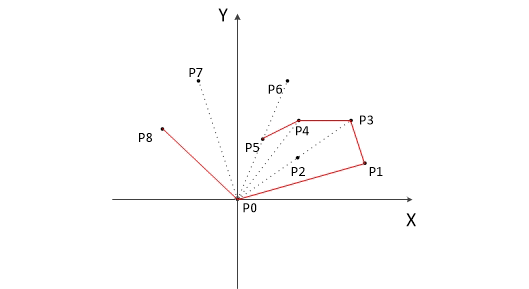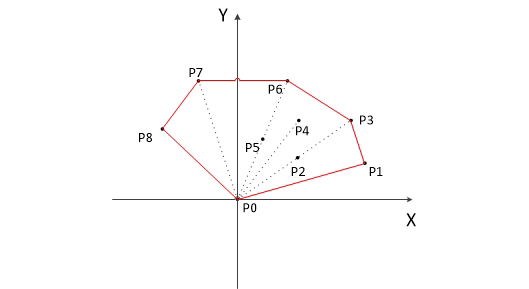
ConvexHull_4

3.1 判断逆时针旋转（Implementing ccw）

给出 3 个点 a，b，c，判断 a->b->c 是否是逆时针旋转
分别算出直线 ab 和 cd 的斜率，通过比较两个斜率决定是否为逆时针旋转
具体算法如下：

CCW. Given three points a, b, and c, is a → b → c a counterclockwise turn?

  • Determinant (or cross product) gives 2x signed area of planar triangle.
    ConvexHull_5
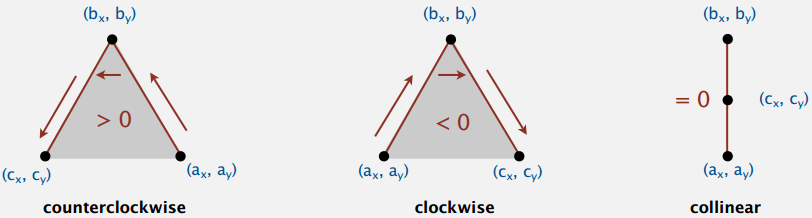
  • If signed area > 0, then a → b → c is counterclockwise.
  • If signed area < 0, then a → b → c is clockwise.
  • If signed area = 0, then a → b → c are collinear.
    ConvexHull_6

3.2 代码

3.2.1 判断逆时针旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Point2D
{
    private final double x;
    private final double y;
    
    public Point2D(double x, double y)
    {
        this.x = x;
        this.y = y;
    }
    
    ...
    
    public static int ccw(Point2D a, Point2D b, Point2D c)
    {
        double area2 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x); // 有浮点数误差的危险
        if      (area2 < 0) return -1; // 顺时针旋转
        else if (area2 > 0) return +1; // 逆时针旋转
        else return 0; // 共线
    }
}

3.2.2 排序

简化假设：不存在三点共线；至少有 3 个点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Stack<Point2D> hull = new Stack<Point>();

Array.sort(p, Point2D.Y_ORDER); // p[0] is now point with lowest y-coordinate
Array.sort(p, p[0].BY_POLAR_ORDER); // sort by polar angle with respect to p[0]

// definitely on hull
hull.push(p[0]);
hull.push(p[1]);

for (int i = 2; i < N; i++) {
    Point2D top = hull.pop();
    while (Point2D.ccw(hull.peek(), top, p[i]) <= 0) // discard points that would create clockwise turn
        top = hull.pop();
    hull.push(top);
    hull.push(p[i]); // add p[i] to putative hull
}

运行时间：排序：NlogN；剩余部分：线性
每个点出入栈最多一次