并查集：渗透问题

发表于 | 分类于

1 渗透（Percolation）

一个N×N的网格，判断顶部和底部是否连通就是渗透问题。[^1]
如图 1，左侧的网格能渗透，右侧的不能渗透。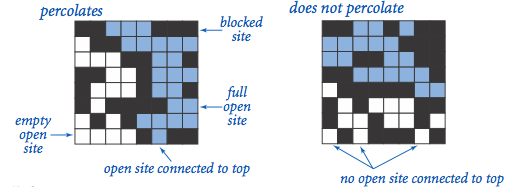
percolates

2 问题（The problem）

假设每个格子打开（白色）的概率是 p（所以关闭（黑色）的概率是 1-p），那么整个系统是渗透的的概率是多少？当 p 为 0，系统一定是非渗透的；当 p 为 1，系统一定是渗透的。图 2 和图 3 分别表示了当网格为 20*20 和 100*100 时， p 与系统渗透的概率之间的关系。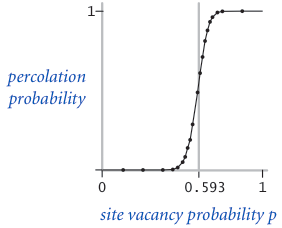
percolates
percolates
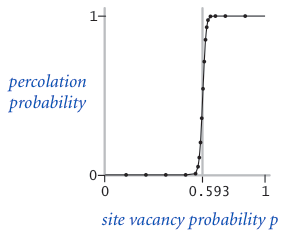
当 N 足够大的时候，我们会得到一个阈值 p*，当 p < p* 时，NxN 的网格几乎不会渗透；当 p > p* 时，NxN 的网格几乎总是渗透。
还没有数学方法可以推断出阈值 p*，但是我们可以通过计算机程序模拟来估算 p*。

3 渗透问题数据结构（Percolation data type）

1
2
3
4
5
6
7
8
9
10
public class Percolation {
   public Percolation(int n)                // 创建一个 n*n 的网格，所以格子都是关闭的
   public void open(int row, int col)       // 如果格子 (row, col) 是关闭的，打开它
   public boolean isOpen(int row, int col)  // 判断格子 (row, col) 是否是打开的
   public boolean isFull(int row, int col)  // 判断格子 (row, col) 是否与网格顶部连通
   public int numberOfOpenSites()           // 打开格子的个数
   public boolean percolates()              // 判断系统是否是渗透的

   public static void main(String[] args)   // test client (optional)
}

3.1 极端案例（Corner cases）

行和列的下标都是从 1 到 n，(1, 1) 是左上角的格子
如果 open()、isOpen()、或者isFull() 的参数超出了规定范围，则抛出异常 java.lang.IndexOutOfBoundsException
如果 n ≤ 0，构造函数抛出异常 java.lang.IllegalArgumentException

3.2 性能要求（Performance requirements）

构造函数时间复杂度为 $n^2$ 的正比
所有方法调用并查集的方法 union()，find()，connected()，count()的次数为常数

4 蒙特卡罗仿真（Monte Carlo simulation）

  • 将所有格子初始化为关闭
  • 重复以下过程直到系统为渗透的
    • 在所有关闭的格子中随机挑选一个
    • 打开它
  • 估算的渗透阈值为：打开的格子数 / 总格子数

举个例子，下面 4 幅图为 20*20 的网格的估算过程，估算的阈值为 204/400 = 0.51
percolation
重复这个过程 T 次，我们可以得到更加精确的渗透阈值。用 $x_t$ 表示第 t 次实验打开的格子数。
$$
\overline{x} = \frac{x_1+x_2+ \cdot\cdot\cdot +x_T}{T}
$$
$$
s^2 = \frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+ \cdot\cdot\cdot +(x_T-\overline{x})^2}{T-1}
$$
当 T 足够大（至少 30），下面这个式子可以为渗透阈值提供 95% 的置信区间
$$
\left[ \overline{x} - \frac{1.96s}{\sqrt{T}}, \overline{x} + \frac{1.96s}{\sqrt{T}} \right]
$$
为了统计多次实验，我们使用以下数据结构：

1
2
3
4
5
6
7
8
9
public class PercolationStats {
   public PercolationStats(int n, int trials)    // 执行 trials 次独立实验，网格为 n*n
   public double mean()                          // 计算渗透阈值的平均数
   public double stddev()                        // 计算渗透阈值的标准差
   public double confidenceLo()                  // 95% 置信区间的左端
   public double confidenceHi()                  // 95% 置信区间的右端

   public static void main(String[] args)        // test client (described below)
}

如果 n ≤ 0 或者 trials ≤ 0，构造函数抛出异常 java.lang.IllegalArgumentException
main()方法有两个参数：n 和 T。使用 n x n 网格进行 T 次独立实验，打印出样本平均值（sample mean）、样本标准差（sample standard deviation）和 95% 的置信区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
% java PercolationStats 200 100
mean                    = 0.5929934999999997
stddev                  = 0.00876990421552567
95% confidence interval = 0.5912745987737567, 0.5947124012262428

% java PercolationStats 200 100
mean                    = 0.592877
stddev                  = 0.009990523717073799
95% confidence interval = 0.5909188573514536, 0.5948351426485464


% java PercolationStats 2 10000
mean                    = 0.666925
stddev                  = 0.11776536521033558
95% confidence interval = 0.6646167988418774, 0.6692332011581226

% java PercolationStats 2 100000
mean                    = 0.6669475
stddev                  = 0.11775205263262094
95% confidence interval = 0.666217665216461, 0.6676773347835391

5 解决方案（Solution）

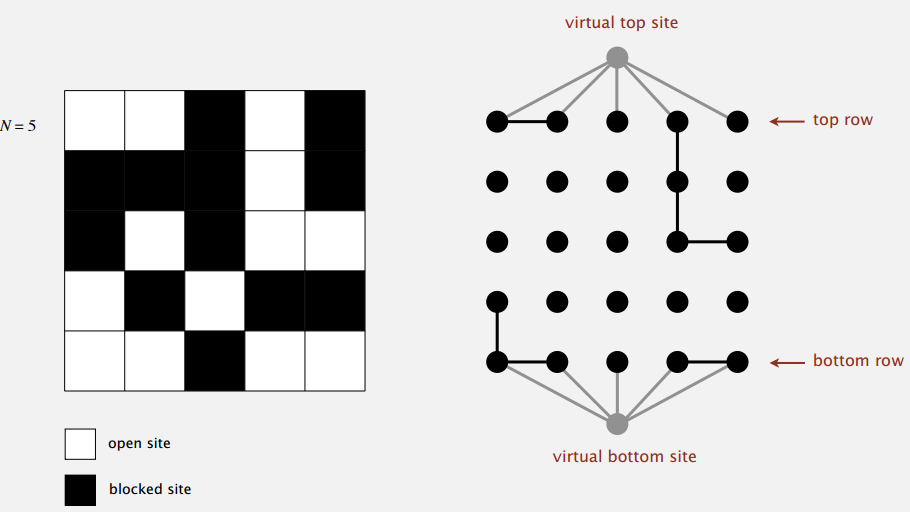
我们可以把这个问题当做一个动态连通性问题来解决。为了计算方便，我们在网格的顶部和底部各加一个虚拟的节点，这样就把渗透问题简化成判断两个节点能否连通。如图 8所示。
DynamicConnectivitySolution

6 代码

见 GitHub 的 repo：PrincetonAlgs4

  • Percolation.java（没有解决 backwash 问题）
  • PercolationStats.java

7 分析运行时间和占用内存（Analysis of running time and memory usage）

见分析报告

[^1]: 原文见 http://coursera.cs.princeton.edu/algs4/assignments/percolation.html
也可从网站 http://introcs.cs.princeton.edu/java/assignments/ 找到