产品推荐

发表于 | 分类于

1 搭建推荐系统（Building a recommender system）

1.1 方案一：流行度（Solution 1：Popularity）

最基本的一种推荐方法是根据每件商品的流行度进行推荐
缺点：缺乏个性化

1.2 方案二：分类模型（Solution 2：Classification model）

根据商品和用户的一些特征来做出推荐

优点：

  • 个性化
  • 可以考虑到具体情景
  • 在用户购物记录很少的情况下，也能运作良好（即使把个人信息作为特征也可以分类）

缺点：

  • 特征可能收集不全（比如：不知道用户的年龄、性别、···；或者商品信息不全）
  • 很多情况下不如协同过滤

1.3 协同过滤（Collaborative filtering）

协同过滤技术为用户做推荐的依据有：其他所有人的历史购物记录、产品推荐的实例、用户和商品的一般化的关联关系
比如：看了这件商品的人还看了···

2 共生矩阵（Co-occurrence matrix）

2.1 共生矩阵（Co-occurrence matrix）

共生矩阵（Co-occurrence matrix）
这个矩阵记录着哪些商品是被相同用户购买的
Cij：代表买了商品 i 也买了商品 j 的人的人数
共生矩阵具有对称性（Symmetric）：Cij=Cji
这样的矩阵是个稀疏矩阵

利用共生矩阵推荐商品（假如用户买了商品 a）：
查找共生矩阵中商品 a 那一行的最大值，它所对应的列即为要推荐的产品

2.2 共生矩阵规格化（Normalize co-occurrences）

当有一种（商品 b）商品非常流行时，用上述方法进行推荐很可能出现不管买了什么商品都会推荐商品 b 的情况出现，所以我们需要让推荐更加个性化

共生矩阵规格化（标准化、正规化）常用的方法之一是Jaccard 相似度（Jaccard similarity）
这与我们在文章《聚类和相似度：检索文档》中所讲的 TF-IDF 非常相似
$$\frac{买了商品i和商品j的人数}{买了商品i或商品j的人数}$$
当然我们也可以用余弦相似度等其他方法

局限：

  1. 只考虑了当前的状态，没有考虑历史状态
    解决方法：将用户的购物历史考虑进来。例如：用户 a 买了商品 a 和商品 b，那么计算是否推荐向用户 a 推荐商品 c 的计算方法是：
    $$ Score(用户a, 商品c)=\frac{1}{2}(Score(商品c, 商品a)+Score(商品c, 商品a)) $$
    分数越高越应该被推荐
    我们也可以对上述方法进行调整，例如不是单纯的计算平均数，而是将更近的购买记录权重设大一点，计算加权平均数
  2. 没有显著地考虑其他因素，例如购买发生的时间段、用户的特征（年龄、性别、···）、商品的特征
  3. 冷启动问题
    当有一个新商品或者新用户时，会遇到冷启动问题

2.3 矩阵分解（Discovering hidden structure by matrix factorization）

在上一节中，我们并没有考虑商品和用户的特征，我们将在本节进行完善
在本节我们使用电影推荐作为案例

2.3.1 矩阵完整性问题（Matrix completion problem）

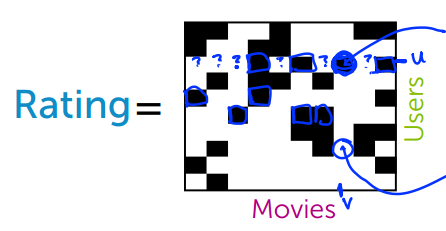
1.3.1 节中的共生矩阵是个稀疏矩阵，如图
RecommendingProducts_1
上图是一个电影评价矩阵，行代表电影，列代表用户，黑色方块代表用户对电影做了评价，白色方块则表示没有评价记录
我们需要根据已有的评价记录来预测未知的评价，即根据黑色方块的信息来填充白色方块

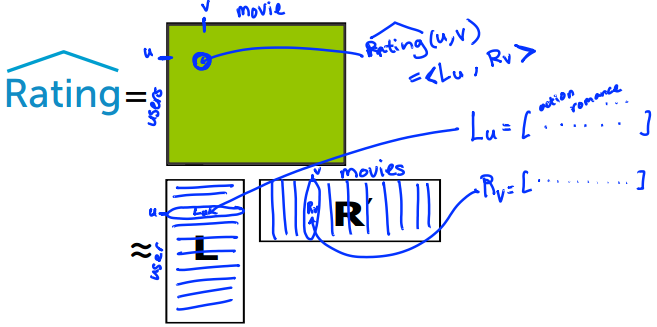
我们可以通过电影的主题和用户喜欢的主题来进行预测[^1]：

  1. 首先设置 d 个主题。例如：action（动作片）、romance（爱情片）、drama（喜剧）
  2. 通过主题描述影片类型。例如：movie v 与动作片的相关值是 0.3，与爱情片的相关值是 0.01，与喜剧片的相关值是 1.5，那么 Rv=[0.3, 0.01, 1.5]
  3. 通过主题描述用户偏好。例如：user u 喜欢动作片的程度为 2.5，喜欢爱情片的程度为 0，喜欢喜剧片的程度为 0.8，那么 Lu=[2.5, 0, 0.8]
  4. 将影片类型向量（**Rv）和用户偏好向量（Lu**）进行比较：
    $$
    \hat{Rating}(u,v) = <\vec{R_v} , \vec{L_u}> = \vec{R_v} \cdot \vec{L_u}
    $$
    例如：预测例子中 user u 喜欢 movie v 的程度：$\hat{Rating}(u,v) = \vec{R_v} \cdot \vec{L_u} = 0.3 \cdot 2.5 + 0.01 \cdot 0 + 1.5 \cdot 0.8 = 1.95$
    当需要推荐电影时，我们将所有被预测过的电影按预测的评价结果进行排序，然后向用户推荐预测评价结果高的电影

2.3.2 基于完整矩阵的预测（Predictions in matrix form）

根据上一节的步骤描述，我们可以得到完整的评价矩阵的计算方法：
$$\hat{Rating} = \vec{R} \cdot \vec{L}$$
如果对矩阵的计算不熟悉的话，可以参考下图：
RecommendingProducts_2

2.3.3 矩阵因式分解模型：发掘隐藏结构（Matrix factorization model: Discovering topics from data）

在 2.3.1 和 2.3.2 小节中，我们对未知评价进行了预测，但有一个问题是：我们事先并不知道用户的偏好和影片的类型，所以本节可以说是前两小节的逆过程——通过已知的评价矩阵（$\vec{Rating}$）来分析用户的偏好矩阵（$\hat{L}$）和影片的类型矩阵（$\hat{R}$）
现在有非常多的方法来计算，其中非常简单的一种方法是：计算残差平方和的最小值
$$
RSS(\vec{R},\vec{L}) = \sum^{v} \sum^{u} (Rating(u,v)-\vec{R_v} \cdot \vec{L_u})^2
$$

这里用到的推理方式称为矩阵因式分解模型（Matrix factorization model），通过把矩阵因式分解的方式来逼近它自身

矩阵因式分解模型的局限：无法解决冷启动问题。当一部电影没有任何数据，或者一个用户没有任何记录时，它将无法补全矩阵

2.3.4 混合模型（Blending models）

其实要想的得到更准确的推荐系统，利用混合模型，将多种模型整合在一起是必不可少的。事实上排在 Netflix Prize 第一的团队整合了 100 多种模型。

3 推荐系统的性能评测（Performance metrics for recommender systems）

3.1 一种推荐系统的性能评测（A performance metric for recommender systems）

为什么我们不能使用分类精度之类的东西来衡量推荐系统的表现呢？

  • 分类准确度 = 正确分类项目数 / 所有项目数，但是在推荐系统中，我们只对用户喜欢商品的数目感兴趣
  • 我们怎样快速地找到用户喜欢的一小部分商品（可能是一个不平衡分类问题）

所以我们将用一种叫做精确度-召回率曲线（Precision-recall curves）的东西来衡量推荐系统的好坏
$$ recall = \frac{用户喜欢并且被推荐的商品数}{用户喜欢的商品总数} $$
所以召回率可以用来衡量被推荐的一组商品在多大程度上覆盖了用户真正喜欢的商品
$$ precision = \frac{用户喜欢并且被推荐的商品数}{被推荐的商品总数} $$
所以精确度可以用来衡量被推荐的一组商品中有多少是用户真正喜欢的

3.2 最佳推荐（Optimal recommenders）

如果想使召回率最大，最简单的办法就是推荐所有商品，此时召回率为 1，但是此时的精确度很小
当然，最佳推荐是推荐且仅推荐用户喜欢的商品此时召回率和精确度都是 1

3.3 精确度-召回率曲线（Precision-recall curves）

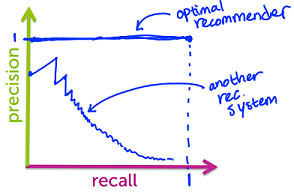
改变推荐数目的阈值，观察曲线的变化
RecommendingProducts_3
如上图所示，理想的曲线是精确度恒为 1 的那条，而实际中曲线往往是锯齿形的
显然，当精确度和召回率都尽量大时，情况更为理想
一种方法是计算曲线与坐标轴围成的图形的面积（area under the curve (AUC)）
另一种情况，当已知推荐数量时，只需找出精确度最大的曲线即可

4 案例研究：推荐歌曲

代码在这里

[^1]: 粗体字母表示向量。例如：R 表示向量R